Note: This article was written while conducting research for the Polis Foundation and was first published on their blog here.
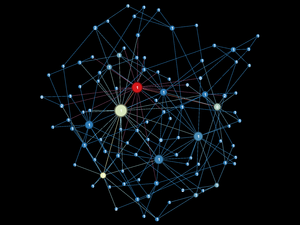
Transitive transaction describes the process whereby two untrusted (unconnected) agents on a network can transact (exchange coins) using their common, mutually trusted connections acting as intermediaries.
The following provides a description of the transitive transaction algorithm Polis uses in our network-based economic modeling (supporting definitions are provided further down).
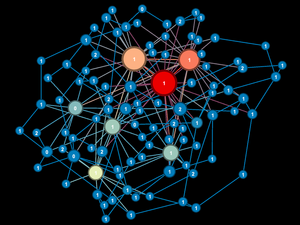
A Buyer agent (B) and a Seller agent (S) are two agents that exist on the same network. They do not have to be neighbors. B wants to buy something from S for a transaction amount (price) P.
Step 1: Find all paths through the network between B and S using the network's Adjacency Matrix as follows:
- Record each of B’s neighbors (connections) as a path
- Recursively search each of B’s neighbors uncommon neighbors (connections) until
a. S is found (a success), or
b. The recursion exceeds a step limit without finding S (a failure), or
c. The path loops back to B before finding S (a failure) - Record all paths found to S
- Sort them from shortest to longest
Step 2: Determine if there is enough liquidity on each path to support the deal
Step 3: If a liquid path is found, record the transaction (writing appropriate transaction records in the ledgers of each agent along the path, including B and S) or record a transaction failure due to insufficient liquidity.
Supporting Definitions
-
Every agent has their own, personal currency. All currencies have the same transfer price, currently zero (not to be confused with the transaction price).
-
An agent A will accept the following types of currency from agent B if A and B are mutually trusted neighbors (connected). A will accept
- B’s currency
- Any of A’s currency B might possess
- Any currency B has from other agents that both A and B trust (are directly connected, named mutually connected agents).
-
Deal liquidity means agent B possesses a basket of currency types that agent A will accept in sufficient quantity to meet or exceed the transaction amount (price).
-
The order for which a bag of currency equalling the transaction amount is passed from B to A is
- If B holds A’s coins, these will be transferred first
- Next, if necessary, coins from mutually connected neighbors will be transferred
- Finally, if necessary, B’s coins will be transferred to A
-
In the case above with B and S transacting, and B and S not being neighbors (being unconnected), these measures of liquidity and rules of coin transfer hold for all agents situated on each segment of the path between B and S. In this case B and S will transact but not not share coins directly, instead a chaining process is performed using the agents along the selected network path that lies between them as intermediaries.
Notes
-
It is by convention only that we use the shortest available liquid path.
-
Similarly, by convension, we use the first liquid path discovered from an ordered list regardless if there are one or more paths of the same length.
-
Similarly, by convension, we adopt the order of coin types transferred from B to A to meet the transaction price.
-
A curious consequence of this apparatus is ones “current balance” is relative, one may have as many “current” balances as one has neighbors.